Is homogenisation of Australian temperature data any good?
Part 2. Marble Bar, the warmest place in Australia
Dr Bill Johnston[1]
Maximum temperature data for Marble Bar exemplifies all that is wrong with the Australian Climate Observations Reference Network – Surface Air Temperature (ACORN-SAT) dataset used to depict Australia’s warming. Subjective adjustments based on faulty metadata and highly correlated comparator sites that likely embed parallel faults results in trends in homogenised data that are unrelated to the climate.
Read on …
Background
Located 150 km southeast of Port Hedland on the edge of the Great Sandy Desert, Marble Bar is reputed to be the warmest place in Australia. The dry season from April to November is extremely dry, while during the ‘wet’, potential evaporation exceeds rainfall even in the wettest month of February. Nevertheless, irregular cyclonic intrusions from the Timor Sea and eastern Indian Ocean can wreak havoc across the Pilbara including at Marble Bar.
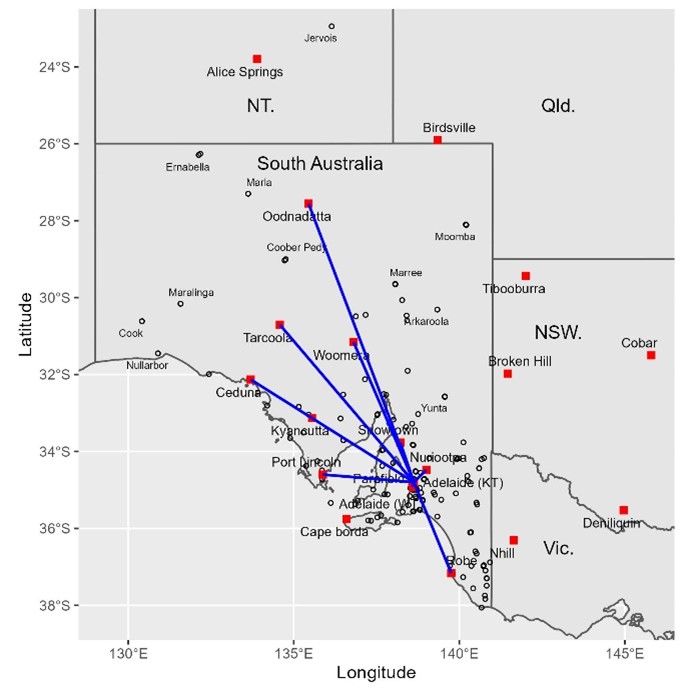
Temperature and rainfall have been measured at several locations under a variety of conditions by post office staff and volunteers since 1901. However, due to its isolation the weather station was rarely inspected by the Bureau of Meteorology (BoM), consequently metadata (data about the data) is unreliable. What was it like ‘doing the met’ under blistering hot conditions and how did equipment including thermometers fare with furnace-like winds, desert dust, and at the other extreme, cold winter nights? Typical of an arid swath of northwestern Australia, Marble Bar is an Australian Climate Observations Reference Network – Surface Air Temperature (ACORN-SAT) dataset used to calculate Australia’s warming (Figure 1).

Figure 1. Marble Bar in relation to other ACORN-SAT sites in northwestern Australia (left), and below, staff outside the original post office in 1900, which was built of local stone (State Library WA).
ACORN-SAT metadata failed to mention that a Stevenson screen was originally supplied in 1911 and that the site moved to the new post office on the corner of Francis and Contest streets in 1948 (Figure 2). Also, that the post office was extended in 1961 to accommodate the telephone line exchange which probably required the Stevenson screen to move up-hill towards the shady watered yard behind the residence. It seems the post office closed in 1984 and its functions including weather observations transferred to the general store opposite the Ironclad Hotel (now licenced post office) 230m east. Later, in 1988 the site allegedly moved east, probably to the Roadhouse, from where it relocated to its current position 100m southwest in 1997.

Figure 2. The side-view of the 1948 post office facing Francis Street (left) photographed in 2016 with the 1961 telephone line exchange annex distant from the camera, and the former residence facing Contest Street (realestate.com.au online sales brochure). Original plans show a path between the residence and the rear of the post office and several out-buildings behind including fuel store, generator/battery shed, and garage.
Objective detection of changes in data using robust statistical methods and post hoc attribution is more reliable than using ACORN-SAT and site summary metadata which is often inaccurate and incomplete. Although now restored, by 1945 the original government offices incorporating the post office had been damaged by cyclones and was riddled with termites. Planned for in 1944, the new post office shown in Figure 2 was not opened until August 1948.
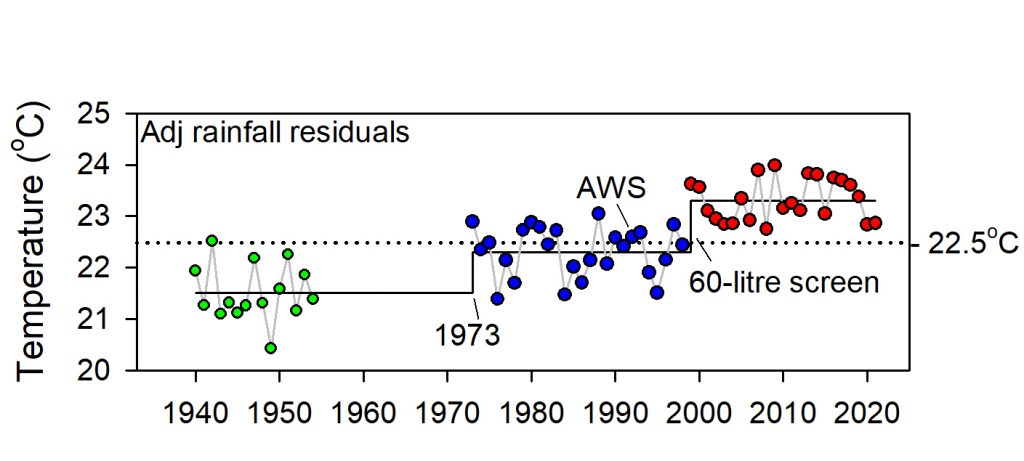
A down-step in Tmax data in 1945, which ACORN-SAT interpreted as site move appeared to be due to observers consistently rounding observations down to the nearest wholeoF, which after converting to Celsius effectively reduced average rainfall-adjusted Tmax by about 0.5oC. While rounding ceased in 1960, data remained cooler than previously until 1988, when it was said the site had become overgrown and was moved “1 km to a residence”. Within that time the Stevenson screen moved clear of the 1961 telephone line exchange, which affected the frequency of high vs low extremes; observations were metricated from 1 September 1972, which affected precision; and in 1984 the site moved to the general store (the current licenced post office), where whole and ½oC were over-reported from 1995 to 1997. It was only after the site relocated in 1998 that data were reasonably consistently observed to the nearest decimal place.
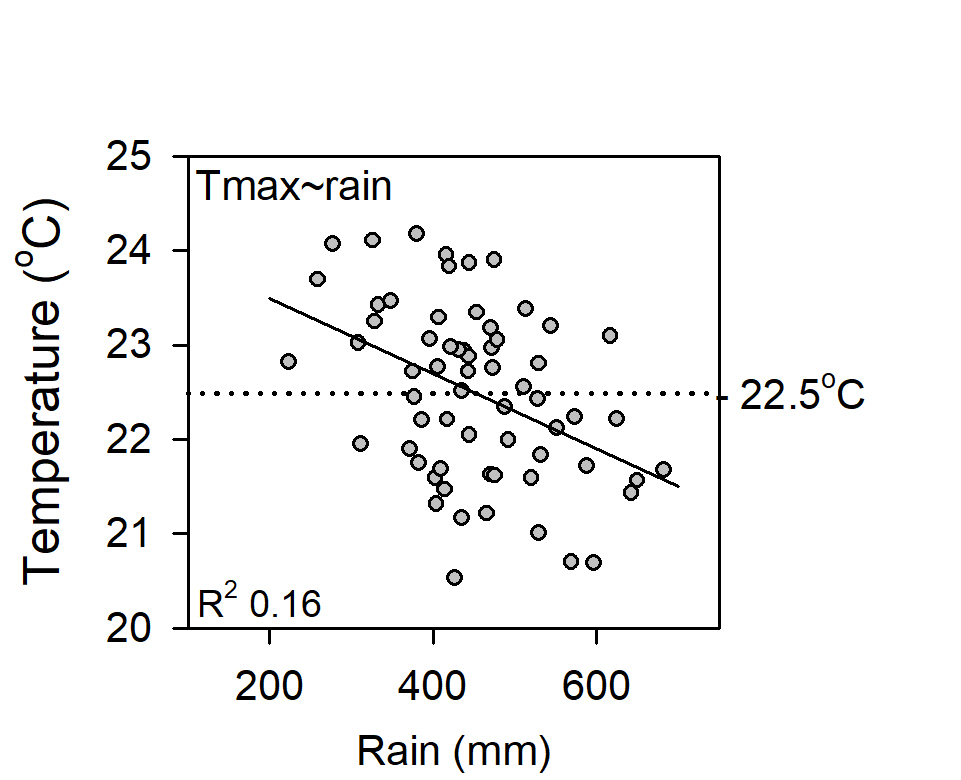
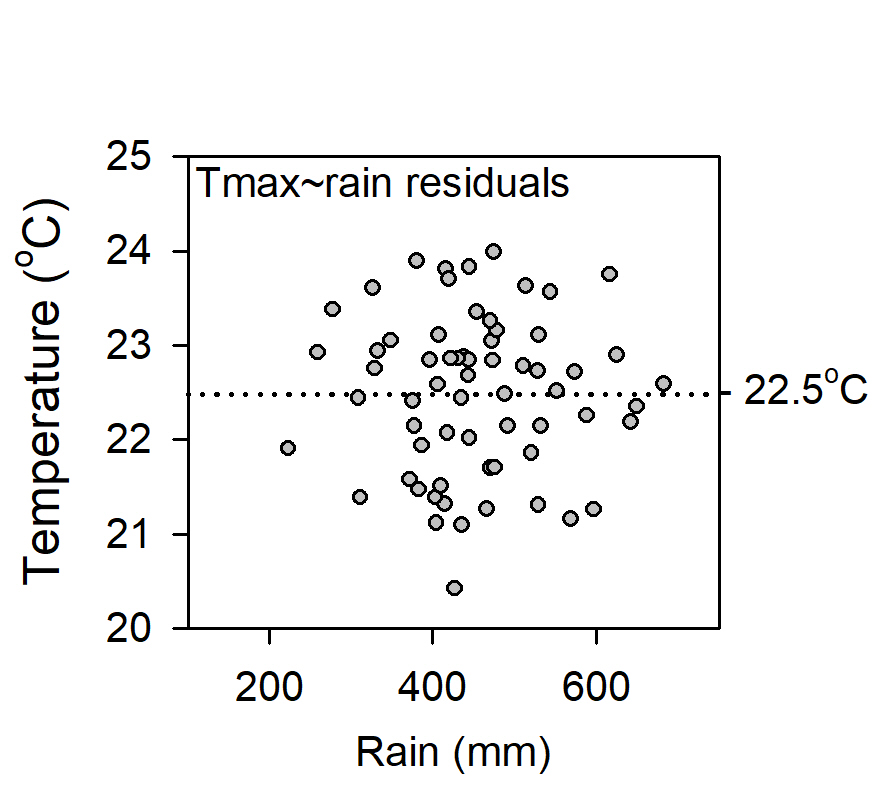
Lack of precision (low R2adj) in the relationship between Tmax, rainfall and site changes, indicates the quality of Marble Bar data is relatively poor. While site changes caused Tmax data to warm 0.9oC since 1901, no warming is attributable to the climate.
Homogenisation
The Bureau’s homogenisation methods are plagued by faulty metadata and the biased selection of neighbouring sites used to make adjustments.
Read on …
The most obvious problems with the Bureau’s temperature homogenisation methods are:
- Metadata for weather stations including Marble Bar is either misleading, scant or non-existent.
- As no weather stations have stayed the same, it is highly likely within regions that many had undergone concurrent changes/upgrades since they were first established. Examples include post-WWII changes at aerodromes in the late 1940s, installing telephone line exchanges at post offices in the 1950s, metrication in 1972, installation of the major trunk network microwave towers in post office yards by Telecom by 1975, the staged introduction of 60-litre Stevenson screens, automatic weather stations etc.
- As many weather stations are affected by synchronous changes and all exhibit similar seasonal cycles, selection of comparator datasets from the pool of possible contenders on the basis of linear correlation of first differences is bound to rank those having parallel faults as candidates for making ACORN-SAT adjustments.
Using faulty metadata to subjectively determine times when something changed, allows changepoints to be manipulated to achieve pre-determined trends. It also discourages further investigation of their cause. For instance, the 1944/1945 down-step at Marble Bar was due to a precision problem not a site move. Other changes included that from 1966 to 1985 the frequency of daily observations greater than 95th day-of-year percentiles was significantly depressed, probably due to watering or shade. Reconstructing what actually happened based on effects observed in data requires changepoints to be identified statistically using robust, statistical methods and post hoc investigation of causes.
Using Pearsons linear correlation to select up to 40 neighbouring sites for constructing comparative reference series is biased. As monthly averages cool from summer to winter and warm from winter to summer, residual cycles in first-differenced data inflate significances of correlations. Thus, from the pool of potential neighbours whose data are not homogeneous, linear correlation is likely to select those having parallel faults. Furthermore, increasing the number of comparators cannot overcome the high likelihood that station changes within regions are somewhat synchronised.
Objective, replicable homogenisation would investigate time-related changes in properties of datasets using objective statistical tests (of which there are a number) and relate changes in the data to what is known about the site post hoc. For example, by comparing detected changepoints with BoM metadata, documents, maps, plans and aerial photographs held by the National Archives and the National Library of Australia, state authorities, museums, historical societies, newspaper reports etc. Even if supporting information is not available, statistical detection based on the probability of an abrupt sustained change against the NULL hypothesis of no change should be sufficient evidence that change occurred.
Historic data were not collected to be used decades in the future to detect trend and change. Due to inaccurate metadata, poor site control (screen and instrument deterioration, watering, shade), and prior to metrication on 1 September 1972, lack of precision by observers, Marble Bar data could not be regarded as high-quality. As the Bureau’s homogenisation methods are deeply flawed the ACORN-SAT project should be abandoned.
Two important links – find out more
First Link: The page you have just read is the basic cover story for the full paper. If you are stimulated to find out more, please link through to the full paper – a scientific Report in downloadable pdf format. This Report contains far more detail including photographs, diagrams, graphs and data and will make compelling reading for those truly interested in the issue.
Click here to download the full paper with photos graphs and data.
Second Link: This link will take you to a downloadable Excel spreadsheet containing a vast number of Marble Bar data points for the years from 1901 to 2020 and which was used in the analysis of the Marble Bar weather records to support the Full Report.
Click here to download the Excel spreadsheet with data points 1901 to 2020
Note: Line numbers are provided in the linked Report for the convenience of fact checkers and others wishing to provide comment. If these comments are of a highly technical nature, relating to precise Bomwatch protocols and statistical procedures, it is requested that you email Dr Bill Johnston directly at scientist@bomwatch.com.au referring to the line number relevant to your comment.
[1] Former NSW Department of Natural Resources research scientist and weather observer.